Vectors are arrows that show both how much and which way a quantity acts, like force or velocity. They help you visualize and analyze movement or forces in physical systems. Each vector has a magnitude (length) and a direction, making it easier to understand how multiple effects combine. By breaking vectors into components, you can simplify calculations and better grasp complex interactions. Keep exploring to learn how these ideas work together in real-world applications.
Key Takeaways
- Vectors are arrows representing quantities with both magnitude and direction.
- They are visualized as arrows pointing in a specific direction with length indicating size.
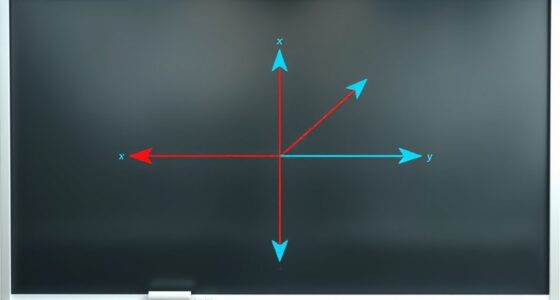
- Vectors can be broken into components along horizontal and vertical axes.
- Adding vectors involves combining their components to find a resultant vector.
- Understanding vectors helps analyze forces, velocities, and movements in physical systems.

Have you ever wondered how to represent movement or force in a precise way? Vectors do just that—they are arrows that encode both the magnitude and direction of a quantity. When working with vectors, you can think of them as tools that help you visualize and analyze physical phenomena, like the force pushing you forward or the velocity of a moving object. One of the foundational concepts in vector analysis is vector addition, which allows you to combine multiple vectors into a single, resultant vector. This process involves adding the vector components—essentially breaking down each vector into its horizontal and vertical parts—and then recombining them to find the overall effect.
Imagine you have two vectors, each representing forces acting on an object. To add these vectors, you first find their components — the horizontal (x) and vertical (y) parts. This step is essential because it simplifies the process, especially when vectors are not aligned along the same line. For example, if one force pushes to the right and slightly upward, and the other pushes to the left and downward, breaking them into components helps you see the combined influence clearly. You can add the x-components together to find the total horizontal effect and do the same with the y-components for the vertical effect. Once you have these sums, you can reconstruct a single vector from these combined components, which represents the net force or movement.
This process, called vector addition, is fundamental because it allows you to understand how multiple vectors interact. It’s especially useful when analyzing real-world problems involving forces, velocities, or displacements. By working with vector components, you avoid complex geometric calculations and instead perform straightforward algebraic operations. The resulting vector from this addition is called the resultant vector, and it provides a complete picture of the overall effect—how strong it is (magnitude) and where it points (direction). You can then use the Pythagorean theorem to find the magnitude and trigonometry to determine the direction, giving you precise control over the analysis. Additionally, understanding vector components is crucial for accurately interpreting the combined effects in various physical and engineering contexts.
Understanding vector addition through components makes working with vectors more manageable and intuitive. It allows you to break complex situations into simple parts, analyze each separately, and then combine them to see the whole picture. Whether you’re calculating forces on a bridge, determining the resultant velocity of an airplane, or analyzing any physical system involving direction and magnitude, mastering vector components and addition provides a powerful foundation. With these tools, you gain a clearer, more precise way to interpret and solve problems involving vectors.
Frequently Asked Questions
How Are Vectors Different From Scalars?
Vectors differ from scalars because they include both magnitude and direction, while scalars only have magnitude. When you use vector notation, like an arrow, it shows the direction and size of the quantity. In a scalar comparison, you’re only considering the amount, such as mass or temperature, without any directional info. So, vectors give you a complete picture, whereas scalars focus on just how much.
Can Vectors Be Negative? How?
Imagine you’re pushing a box north, but then you push south with more force. In vector notation, this results in negative vectors, which mean the vector points in the opposite direction. Yes, vectors can be negative, indicating direction. When representing them, you might see a minus sign before the vector. Negative vectors fundamentally show movement or force opposite to the chosen positive direction, helping you understand real-world situations more clearly.
What Is the Significance of Vector Magnitude?
The significance of vector magnitude is that it tells you the vector’s length, which represents its size or strength. You calculate the magnitude by finding the vector’s length using the magnitude calculation, typically involving the square root of the sum of squared components. This measurement helps you understand how much influence or effect the vector has, regardless of its direction, making it essential for precise analysis in physics and engineering.
How Do Vectors Combine Through Addition?
Imagine vectors as tiny, rebellious arrows that refuse to stay in line. When you add vectors, you’re basically doing a vector resolution, breaking them into components and summing each part. By combining their components—horizontal and vertical—you get a new resultant vector. It’s like a coordinate dance—adding each step to reach your final destination. So, embrace the chaos of vector components, and watch your vectors unite beautifully.
Are Vectors Only Useful in Physics?
Vectors aren’t only useful in physics; you can see their applications in many fields like engineering, computer graphics, and navigation. They help visualize forces, velocities, and directions through vector visualization, making complex concepts easier to understand. You’ll find vectors essential for analyzing movements, designing systems, or even understanding data trends. Their versatility makes them a powerful tool across various disciplines, not just in physics.
Conclusion
Now that you know the basics of vectors—arrows with magnitude and direction—you’re well on your way to mastering motion and measurement. Remember, vectors vividly visualize velocity, force, and more, making complex concepts clearer. Keep practicing, and you’ll soon see how simple yet powerful these pointers are. With curiosity and confidence, you can conquer concepts, create clarity, and continue your journey in understanding the fascinating world of vectors!