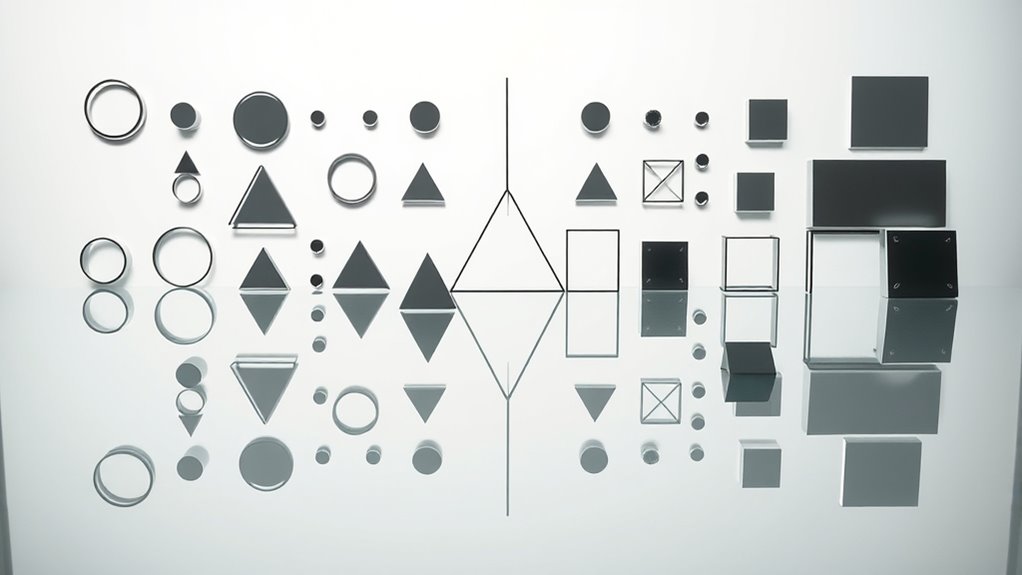
In geometry, symmetry helps you understand how shapes are balanced and structured. You’ll learn about two main types: rotational symmetry, where a shape looks the same after a rotation, and line reflection, where shapes are flipped across a line like a mirror. Recognizing these patterns helps reveal hidden order and beauty in objects. Keep exploring, and you’ll discover even more about how symmetry influences the shapes and patterns around you.
Key Takeaways
- Symmetry in geometry includes rotational symmetry (shape looks the same after rotation) and line reflection (mirror image across a line).
- Rotational symmetry’s order indicates how many times a shape matches itself during a full 360° turn.
- Line reflection, or mirror symmetry, involves flipping a shape across a line so the image is a mirror of the original.
- Many shapes and objects display symmetry, contributing to visual balance, aesthetic appeal, and pattern recognition.
- Understanding symmetry helps analyze shape properties, patterns, and their applications in art, design, and natural forms.

Have you ever wondered how shapes and sizes are measured and understood? When exploring the world of geometry, one of the first concepts you’ll encounter is symmetry. Symmetry helps us understand how shapes can be balanced and how they relate to themselves through specific transformations. Two fundamental types of symmetry are rotational symmetry and line reflection, each offering a different way to see how shapes can be mirrored or spun around.
Rotational symmetry occurs when you can rotate a shape around a fixed point, called the center of rotation, and the shape looks exactly the same as it did before the rotation. Imagine spinning a star or a snowflake; if it looks identical after a certain degree of rotation, it has rotational symmetry. The number of times a shape matches itself during a full 360-degree turn is called its order of rotational symmetry. For example, a square has rotational symmetry of order 4 because it looks the same every 90 degrees, while an equilateral triangle has an order of 3, matching itself after each 120-degree turn. Recognizing rotational symmetry helps you understand the inherent balance within shapes and how they repeat their pattern through spinning. Understanding symmetry can also be useful in art and design, where visual harmony is important.
Line reflection, on the other hand, involves flipping a shape across a straight line, called the line of reflection, to produce a mirror image. When you reflect a shape across this line, every point of the shape is mapped to a corresponding point on the opposite side, maintaining the same distance from the line. If the original shape and its reflected image are identical, the shape is said to have line symmetry. For example, a butterfly’s wings are often mirror images of each other across a central line, illustrating line reflection. Many everyday objects, like leaves or certain logos, display this kind of symmetry, making them visually appealing and balanced.
Understanding these concepts allows you to analyze and identify symmetrical properties in different shapes and objects. Recognizing rotational symmetry and line reflection isn’t just about aesthetics—it’s also about understanding structure and balance in both natural and man-made forms. Whether you’re designing, drawing, or simply observing, knowing how to spot symmetry helps you see the harmony in shapes around you. It also forms the foundation for more advanced topics in geometry, like tessellations and fractals, where symmetry plays a vital role. So, next time you see a pattern or a shape, think about its lines of reflection and how many times it can spin and still look the same—these insights reveal the hidden order and beauty that geometry offers in the world around you.
Frequently Asked Questions
How Do Symmetry and Reflection Apply to Real-World Architecture?
You see symmetry and reflection in architecture to enhance aesthetic appeal and guarantee structural stability. Symmetrical designs create visual harmony, making buildings more attractive and balanced. Reflections help architects develop mirrored facades, which can improve aerodynamics and load distribution. By applying these principles, you can design structures that are both visually pleasing and resilient, blending beauty with functionality seamlessly in real-world architecture.
Can a Shape Have Multiple Lines of Symmetry? How?
Yes, a shape can have multiple lines of symmetry. When a shape has several lines of symmetry, it means you can perform multiple reflections across those lines, and the shape will look the same. For example, a square has four lines of symmetry, allowing multiple reflections that maintain its shape. This property helps you understand how symmetry works and how different shapes can have various lines of symmetry, making patterns and designs more interesting.
What Is the Difference Between Reflection Symmetry and Rotational Symmetry?
Reflection symmetry involves a shape looking the same after a mirror-like reflection across a line called a line of symmetry. Rotational symmetry means a shape looks the same after rotating it around a central point by a certain angle less than 360 degrees. The key difference is that reflection symmetry uses reflection types as symmetry operations, while rotational symmetry relies on turning the shape around a point. Both demonstrate how shapes maintain their appearance through symmetry operations.
How Do You Find the Line of Symmetry in Complex Shapes?
Finding the line of symmetry in complex shapes might seem like searching for a needle in a haystack, but it’s easier than you think! Look for mirror images on either side of an imaginary line. Break the shape into smaller parts if needed. Remember, symmetry in nature often reveals hidden lines—so study those patterns. Use folding or tracing to confirm your line, and you’ll reveal the shape’s perfect balance!
Are There Shapes With No Lines of Symmetry? Which Ones?
Yes, some irregular polygons and asymmetrical shapes have no lines of symmetry. For example, an irregular scalene triangle or an irregular pentagon doesn’t have any lines that divide it into mirrored halves. You’ll find that these shapes lack symmetry because their sides and angles aren’t equal or evenly balanced. When you analyze such shapes, it’s clear that they don’t have any lines of symmetry, making them asymmetrical.
Conclusion
Now that you understand symmetry and reflections, you can see how shapes mirror each other perfectly. You might think it’s too complicated, but with a little practice, it becomes easier to spot these patterns. Remember, symmetry isn’t just about beauty—it’s a fundamental part of geometry that helps you understand shapes better. Keep exploring, and soon you’ll find that reflecting shapes is just like seeing a fun puzzle unfold before your eyes.