Coordinate and Euclidean geometries are two ways to explore shapes and space. In coordinate geometry, you use algebra and axes to describe and manipulate shapes precisely, making transformations straightforward. Euclidean geometry relies on visual reasoning and constructions without numbers. Both approaches help you understand geometry deeply; one focuses on calculations, the other on properties and constructions. If you keep investigating, you’ll uncover how these perspectives complement each other in many applications.
Key Takeaways
- Coordinate geometry uses algebraic equations and transformations, while Euclidean geometry relies on visual reasoning and constructions.
- Coordinate geometry offers precise calculations and is ideal for applications like computer graphics and engineering; Euclidean geometry emphasizes shape properties and proofs.
- Transformations such as translation, rotation, and reflection are algebraically represented in coordinate geometry, whereas Euclidean methods use geometric constructions.
- Coordinate geometry describes shapes within a coordinate system, enabling easy computation and manipulation; Euclidean geometry focuses on intrinsic properties without coordinates.
- Both perspectives complement each other, with coordinate geometry providing precision and Euclidean geometry offering foundational understanding and intuition.
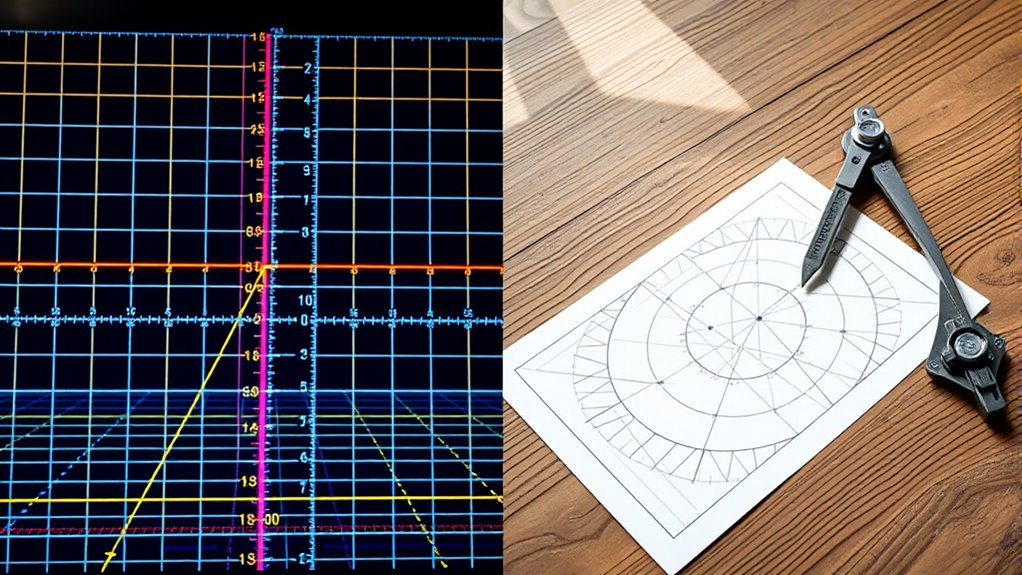
When exploring geometry, you’ll often encounter two fundamental approaches: coordinate geometry and Euclidean geometry. Understanding how these perspectives differ helps you grasp the versatility of geometric concepts and how they apply across various contexts. Coordinate geometry, also known as analytic geometry, relies on a grid system of axes to represent points, lines, and shapes with numerical coordinates. This method allows you to describe geometric entities precisely using algebraic equations, making it especially useful for calculations, plotting, and computer graphics. For example, translating a shape involves adding a vector to each point, shifting it without altering its size or shape. Rotations, reflections, and dilations—forms of geometric transformations—are all expressed through algebraic formulas that manipulate these vectors. This algebraic approach simplifies complex transformations and makes it easier to perform calculations, especially with the aid of technology. Additionally, vector representation plays a central role in coordinate geometry, providing a powerful tool to analyze and perform geometric transformations.
Coordinate geometry uses axes and algebra for precise, calculable shapes, while Euclidean geometry relies on visual reasoning and constructions.
Euclidean geometry emphasizes the intrinsic properties of shapes, such as angles, side lengths, and congruence, without necessarily translating them into numerical coordinates. Instead, it uses geometric constructions and logical reasoning to prove relationships and theorems. For instance, you might use compass and straightedge constructions to demonstrate that two triangles are similar or that a certain angle bisects a segment. Although it’s more visual and less reliant on algebra, Euclidean geometry provides a foundation for understanding the fundamental principles of shape and space.
Both approaches are valuable, but they serve different purposes. Coordinate geometry offers precision and computational power, making it ideal for applications like CAD, physics, and engineering. Euclidean geometry provides deep insight into the properties and relationships within shapes, which is essential for proofs and theoretical understanding. By understanding vector representation and how geometric transformations work within the coordinate framework, you can more easily manipulate and analyze shapes. Meanwhile, Euclidean methods remind you of the pure geometric intuition rooted in classic constructions and logical deductions. Together, these perspectives give you a holistic toolkit for exploring and applying geometry in diverse fields.
Frequently Asked Questions
How Do Coordinate and Euclidean Geometries Relate Mathematically?
You understand that coordinate and Euclidean geometries relate through algebraic representations of geometric concepts. In coordinate geometry, you use points, lines, and shapes with coordinates, enabling precise descriptions. You perform geometric transformations like translations and rotations algebraically, bridging the gap between pure Euclidean ideas and coordinate systems. This connection allows you to analyze and manipulate geometric figures more easily, combining visual intuition with algebraic precision for a thorough understanding.
What Are Practical Applications of Each Geometry Type?
Imagine you’re using a GPS app on your smartphone—it’s like stepping into a sci-fi movie! Coordinate geometry helps in mapping applications by pinpointing exact locations, making orienting seamless. Euclidean geometry aids in designing accurate maps and understanding spatial relationships. Whether you’re navigating city streets or plotting a drone’s flight path, these geometries power practical tools that keep you connected and on course in everyday life.
Can These Geometries Be Combined in Advanced Problem-Solving?
Yes, you can combine these geometries in advanced problem-solving. By using algebraic methods, you translate geometric concepts into equations, making it easier to analyze complex shapes and relationships. Geometric transformations help you manipulate figures, revealing properties or solutions. This integration allows you to leverage the strengths of both perspectives, solving intricate problems more efficiently and gaining deeper insights into geometric structures and their real-world applications.
How Do Coordinate Systems Influence Geometric Interpretations?
Think of coordinate systems as your map in a vast landscape, guiding your understanding through graphical visualization and dimensional analysis. They influence your geometric interpretations by providing a clear framework to analyze shapes, distances, and angles precisely. With coordinates, you can see the bigger picture, making complex concepts more tangible. They turn abstract ideas into visual cues, helping you navigate and solve problems with confidence and clarity.
What Are Common Misconceptions About Euclidean and Coordinate Geometry?
A common misconception is that Euclidean and coordinate geometry are entirely different, but they’re closely related. You might think coordinate systems always provide perfect clarity, yet they can cause visualization errors if you’re not careful. Misunderstanding the relationship between these perspectives can lead to clarity issues. Remember, coordinate geometry helps visualize Euclidean concepts, but it’s essential to understand their differences and limitations to avoid misconceptions.
Conclusion
As you explore the subtle differences between coordinate and Euclidean geometry, you’ll find each offers its own unique charm. While coordinate geometry provides a modern, flexible lens, Euclidean geometry invites you to appreciate timeless, classical insights. Embracing both perspectives gently enriches your understanding, allowing you to see the beauty in their harmony. Ultimately, blending these views softly guides you toward a deeper appreciation of the geometric world around you.









