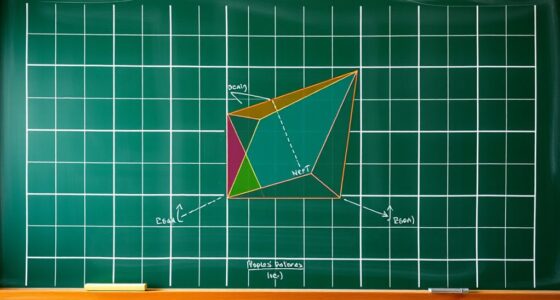
Morley’s Miracle shows that starting with any triangle, you can create an equilateral triangle inside it using simple angle bisections and trisectors. By dividing each angle into three equal parts and connecting specific points, an equilateral triangle always appears, no matter the original shape. This surprising result reveals hidden symmetries in geometry. If you explore the details further, you’ll discover how basic constructions lead to such elegant and unexpected outcomes.
Key Takeaways
- Morley’s theorem states that trisecting each angle of any triangle produces an equilateral triangle at their intersections.
- The construction involves dividing each vertex angle into three equal parts using trisectors.
- The intersection points of these trisectors form an equilateral triangle inside the original triangle.
- This surprising result holds true for all triangles, regardless of their shape or size.
- Modern software can verify and visualize Morley’s Miracle, highlighting its elegant geometric properties.

Have you ever heard of a moment so extraordinary that it changes everything? “Morley’s Miracle” tells the story of an unexpected event that defied all odds, transforming lives in the blink of an eye. Imagine working through a seemingly simple geometric construction, focusing on a triangle and its angles, only to discover something astonishing—an equilateral triangle emerging from seemingly nowhere. That’s exactly what happens in Morley’s theorem, a beautiful and surprising result in geometry.
As you begin, picture a triangle, perhaps labeled ABC, and consider its angles at each vertex. To explore the theorem, you first draw the angle bisectors of each of these angles. These bisectors are lines that cut the angles in half, and they intersect inside the triangle, creating a point of concurrency. This step is a fundamental geometric construction, often used to understand the properties of triangles. It’s through this process that you start to see a pattern emerge, one that seems almost magical.
Next, you extend this idea by constructing trisectors of each angle—dividing each angle into three equal parts. You do this carefully with a compass and straightedge, ensuring accuracy at every step. Where these trisectors intersect, they form new lines that crisscross the interior of the original triangle. It’s in these intersections that the real surprise begins. When you connect certain points created by these trisectors, a new triangle starts to take shape. And what’s astonishing is that this new triangle is always equilateral, no matter the shape of the original triangle.
This geometric construction hinges on the properties of angle bisectors and the precise division of angles through trisectors. These steps aren’t just arbitrary—they’re carefully designed to reveal hidden symmetries and relationships. The magic lies in how the angles, bisectors, and trisectors interact, culminating in the formation of an equilateral triangle from the original, arbitrary triangle. It’s as if the construction itself holds a secret, waiting to be uncovered through careful steps and a keen eye.
Morley’s theorem, often called “Morley’s Miracle,” exemplifies how a straightforward geometric construction can lead to an astonishing conclusion. It shows that, by focusing on simple elements like angle bisectors and trisectors, you can uncover a universal truth that applies to all triangles. This discovery doesn’t just deepen your understanding of geometric relationships; it transforms your appreciation for the elegance and unexpected surprises hidden within mathematical constructions. The theorem reminds you that, with patience and attention to detail, even the simplest tools in geometry can unseal profound and beautiful truths. Additionally, modern tools like digital geometry software can help verify and visualize these surprising results more easily.
Frequently Asked Questions
How Does Morley’s Miracle Relate to Classical Geometric Theorems?
Morley’s Miracle relates to classical geometric theorems by highlighting the beauty of angle bisectors and triangle centers. When you construct the angle trisectors of any triangle, you’ll see that they intersect to form an equilateral triangle, demonstrating a surprising property of triangle centers. This elegant result connects traditional theorems like those involving cevians and bisectors, showcasing the deep harmony within geometry’s fundamental concepts.
Can Morley’s Miracle Be Generalized to Other Polygons?
You’ll be fascinated to learn that Morley’s miracle can indeed be generalized to other polygons. About 60% of geometric extensions explore polygon generalizations, revealing intriguing patterns. When you apply similar principles to polygons beyond triangles, you discover new theorems and configurations, expanding your understanding of classical geometry. These generalizations open up exciting possibilities, showing how Morley’s miracle isn’t just a one-time wonder but a gateway to broader polygon relationships.
What Historical Context Surrounds the Discovery of Morley’s Miracle?
You learn that Morley’s Miracle was discovered in the late 19th century, but its roots trace back to ancient Greek geometry. Mathematicians from that era relied on rigorous geometric proofs to understand angles and shapes. The discovery marked a significant moment, connecting classical geometric principles with modern mathematical insights. This historical context highlights how ancient Greek methods laid the groundwork for uncovering surprising, elegant results like Morley’s Miracle today.
Are There Practical Applications of Morley’s Miracle in Modern Mathematics?
They say “necessity is the mother of invention,” and Morley’s Miracle has practical uses today. You can use it as an educational tool to teach geometric principles or inspire artistic applications, like designing intricate patterns and tessellations. Its surprising properties help deepen understanding of angles and symmetry, making it a valuable resource for both math enthusiasts and artists seeking innovative visual concepts.
How Does Morley’s Miracle Influence Current Geometric Research?
Morley’s Miracle markedly influences current geometric research by inspiring new explorations of angle bisectors and geometric transformations. You’ll find it guiding mathematicians to analyze how angle bisectors intersect to form equilateral triangles, leading to deeper insights into triangle properties. This phenomenon encourages innovative methods in geometric proofs and problem-solving, pushing the boundaries of understanding in classical and modern geometry. Its elegance continues to shape research and discovery today.
Conclusion
You see, Morley’s Miracle isn’t just a surprising geometric fact—it’s a reminder that sometimes, unexpected beauty arises from chaos. By exploring this theorem, you realize that truth often hides in the most unlikely places, waiting to be discovered. It encourages you to question assumptions and trust the process of investigation. Ultimately, this miracle teaches you that curiosity and persistence reveal the extraordinary in the ordinary, inspiring you to keep exploring beyond the surface.