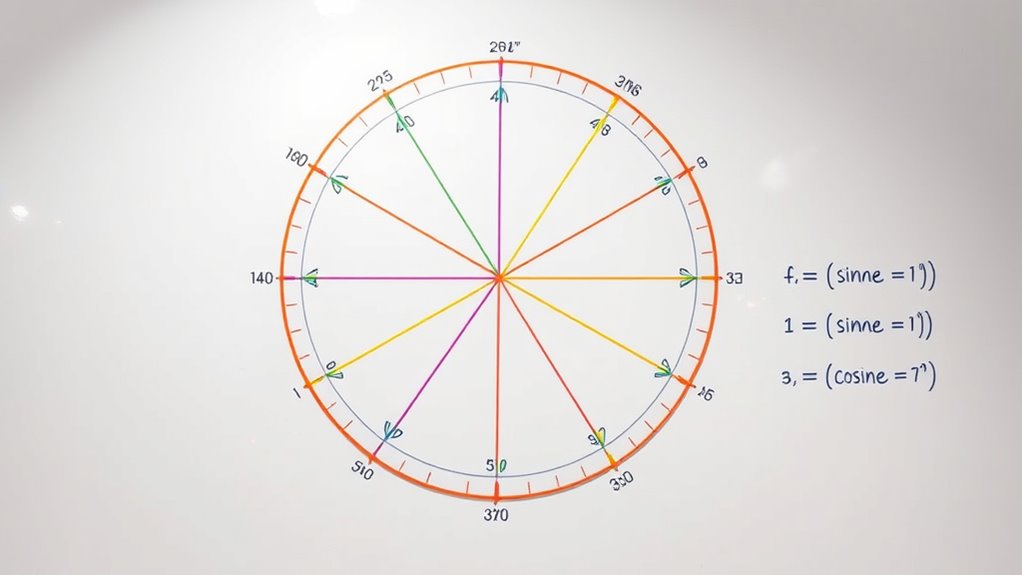
The unit circle is a helpful visual tool that links angles to their corresponding coordinates, making trigonometry easier to understand. By moving around the circle, you can see how angles relate to points, where cosine equals the x-coordinate and sine equals the y-coordinate. This connection helps you visualize sine, cosine, and tangent functions effortlessly. Keep exploring, and you’ll discover more ways this circle simplifies understanding and working with angles.
Key Takeaways
- The unit circle is a circle of radius 1 centered at the origin, used to visualize angles and trigonometric functions.
- Coordinates on the circle at a given angle represent cosine (x-value) and sine (y-value).
- Moving around the circle shows how sine and cosine values change with different angles.
- The unit circle illustrates the periodicity and symmetry of sine, cosine, and tangent functions.
- Understanding the circle helps in solving trigonometric problems and interpreting angles geometrically.
Have you ever wondered how angles and coordinates relate on the unit circle? It’s a fascinating connection that forms the foundation of trigonometry. The unit circle, a circle with a radius of 1 centered at the origin of a coordinate system, provides a visual way to understand how angles translate into specific points on a plane. When you measure an angle from the positive x-axis, the point where the terminal side of the angle intersects the circle gives you essential information about the values of trigonometric functions like sine, cosine, and tangent. These functions are directly tied to the coordinates of that point, making the unit circle a powerful tool for visualizing and calculating trigonometric relationships.
Think of the coordinate system as your map on which the unit circle is drawn. Every point on the circle corresponds to a specific angle, measured in radians or degrees, starting from 0 at the positive x-axis. When you move along the circle, the x-coordinate of the point represents the cosine of the angle, while the y-coordinate corresponds to the sine. This direct relationship means that as the angle changes, the point moves smoothly around the circle, and the sine and cosine values change accordingly. For example, at 0°, the point is at (1, 0), so cosine is 1 and sine is 0. At 90°, the point is at (0, 1), making sine 1 and cosine 0. These coordinates encapsulate the essence of the trigonometric functions and make calculations more intuitive. Recognizing the periodic nature of these functions helps you understand how they repeat their values every 2π radians, which is fundamental in trigonometry.
Frequently Asked Questions
How Do I Memorize All the Coordinates Quickly?
To memorize all the coordinates quickly, use mnemonic devices and flashcard routines. Create catchy phrases to remember key points, like “All Students Take Calculus” for the quadrants. Regularly review flashcards with angles and their coordinates, testing yourself daily. Breaking the task into small parts and repeating these routines helps reinforce memory. Stay consistent, and over time, you’ll recall the coordinates effortlessly without needing to memorize everything at once.
What Are the Real-World Applications of the Unit Circle?
Think of the unit circle as a compass guiding your way through engineering design and computer graphics. It helps you determine angles and coordinates efficiently, making it essential for creating precise models and animations. Engineers use it to analyze wave patterns, while graphics designers rely on it to position objects accurately. Its real-world applications streamline complex calculations, turning abstract math into tangible, visual solutions that bring ideas to life.
How Does the Unit Circle Relate to Sine and Cosine Graphs?
You can see how the unit circle relates to sine and cosine graphs through angle relationships and coordinate visualization. As you move around the circle, the x-coordinate represents cosine, and the y-coordinate represents sine. This connection helps you understand how these functions oscillate periodically. By studying the circle, you easily visualize how sine and cosine graphs mirror the circle’s movement, making complex wave patterns clearer and more intuitive.
Can I Use the Unit Circle for Negative Angles?
Yes, you can use the unit circle for negative angles. Negative angles represent clockwise rotations, and you can find their coordinates by applying unit circle transformations. Simply move clockwise from the positive x-axis, and the corresponding sine and cosine values match the points on the circle, just reflected across the x-axis. This way, negative angles help you understand the full range of circle transformations and trigonometric functions.
What Is the Significance of Special Angles Like 30°, 45°, and 60°?
Think of special angles like 30°, 45°, and 60° as the secret keys to a treasure chest of key ratios. Their significance lies in providing quick, reliable values for sine, cosine, and tangent, making calculations easier. These angles help you master the unit circle’s geometry, giving you a toolkit for understanding angles’ properties and simplifying complex problems. Knowing them is like having a map to mathematical success.
Conclusion
Think of the unit circle as your map through a vast landscape of angles and coordinates. With this guide in hand, you can navigate any problem with confidence, like a traveler finding their way through familiar territory. Remember, each point on the circle open up a new perspective, turning complex concepts into simple steps. Embrace this tool, and you’ll find yourself sailing smoothly across the mathematical terrain, confident in your understanding of angles and coordinates.