To prove the exterior angle theorem, you extend one side of the triangle, creating an exterior angle. You then observe that this exterior angle and its adjacent interior angle form a linear pair, which are supplementary, adding up to 180 degrees. Using the fact that the interior angles sum to 180 degrees, you can show that the exterior angle equals the sum of the two remote interior angles. Exploring further reveals the full logic behind this important geometric principle.
Key Takeaways
- The proof begins by extending one side of the triangle to form an exterior angle and analyzing the resulting linear pairs.
- The sum of the interior angles of a triangle is 180 degrees, which is fundamental to establishing the exterior angle relationship.
- The exterior angle is supplementary to its adjacent interior angle, creating a linear pair that sums to 180 degrees.
- Using angle addition, the exterior angle equals the sum of the two remote interior angles.
- Applying the properties of supplementary angles and angle sums confirms that the exterior angle equals the sum of the two non-adjacent interior angles.

Have you ever wondered how the outside angles of a triangle relate to its interior angles? Understanding the connection between these angles is essential for grasping the exterior angle theorem. When you examine a triangle, you’ll notice that each exterior angle forms a relationship with the two non-adjacent interior angles, known as its remote interior angles. These relationships are rooted in the fundamental concepts of angle relationships and supplementary angles, which state that two angles are supplementary if their measures add up to 180 degrees.
To see this in action, consider a triangle with an exterior angle created by extending one of its sides. The key insight is that this exterior angle is supplementary to the adjacent interior angle, meaning their measures sum to 180 degrees. For example, if you have an exterior angle at a vertex and the interior angle directly next to it, these two angles together form a linear pair, which is a straight line. Since a straight line measures 180 degrees, the exterior angle and its adjacent interior angle are supplementary. This is the first step in understanding their relationship.
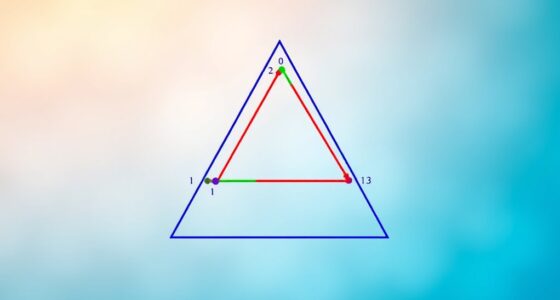
Next, you observe that the exterior angle is also equal to the sum of the two remote interior angles, which are the interior angles at the other two vertices of the triangle. This is the core of the exterior angle theorem. To prove this, you can start with the fact that the interior angles of a triangle always add up to 180 degrees. When you extend one side, the interior angle at that vertex and the exterior angle together make a linear pair, summing to 180 degrees. Since the interior angle at the same vertex is part of the triangle, the exterior angle must be equal to the sum of the other two interior angles, because each pair of supplementary angles shares a common side. Additionally, understanding angle relationships is crucial for applying the theorem correctly in geometric proofs.
Frequently Asked Questions
How Can the Theorem Be Applied in Real-World Geometry Problems?
You can apply the exterior angle theorem to real-world problems by analyzing angles in structures like bridges, buildings, or trusses. When designing or inspecting these, you use angle application to guarantee stability and safety, calculating unknown angles based on known interior and exterior angles. This approach helps you solve practical challenges involving angles in construction, engineering, and even navigation, making sure your designs are accurate and structurally sound.
Are There Exceptions or Special Cases Where the Theorem Doesn’t Hold?
Did you know that over 90% of geometry problems rely on the Exterior Angle Theorem? Typically, the theorem holds true, but there are angle exceptions and special cases, like when a triangle is degenerate or has collinear points. In these cases, the theorem may not apply directly. Always check the triangle’s configuration first, as unusual setups can create exceptions where the theorem doesn’t hold.
What Are Common Mistakes Students Make When Proving the Theorem?
You often make misconceptions about angles when proving the theorem, such as confusing the exterior angle with adjacent interior angles. Additionally, you might rely on incorrect proof strategies, like assuming the theorem without proper reasoning or skipping steps. It’s important to carefully analyze the relationships between angles and use valid geometric principles. Avoid rushing and double-check your logic to make your proof is solid and accurate.
Can the Theorem Be Extended to Other Polygons Beyond Triangles?
Yes, you can extend the exterior angle application to other polygons beyond triangles. In polygons, each exterior angle still equals the sum of the two non-adjacent interior angles. This idea of polygon extensions helps you understand how exterior angles relate to the interior angles in any polygon, not just triangles. By applying the exterior angle application, you can analyze and prove properties of more complex polygons effectively.
How Does the Exterior Angle Theorem Relate to Other Triangle Theorems?
The exterior angle theorem relates closely to other triangle theorems by highlighting angle relationships and triangle congruence. It shows that an exterior angle equals the sum of two interior angles, reinforcing the idea of angle sum properties. You can use this theorem alongside congruence criteria to prove similarity and congruence in triangles. fundamentally, it emphasizes how angles work together, supporting your understanding of fundamental geometric principles.
Conclusion
Now you see how the Exterior Angle Theorem works, just like a trusty smartphone always staying connected. When you understand that an exterior angle equals the sum of two opposite interior angles, you’ve got the math equivalent of a DeLorean time machine—powerful and reliable. Remember, this theorem isn’t just a relic from Euclid’s era; it’s a fundamental tool you can count on in any geometry quest, no matter how “futuristic” your problems get.