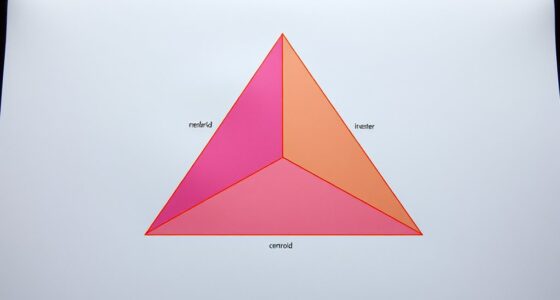
Euler’s line appears in many triangles when the centroid, orthocenter, and circumcenter align in a straight line. This alignment happens in all non-equilateral triangles, with their positions shifting based on the triangle’s angles. In equilateral triangles, these points coincide at the same spot, so the line collapses. Understanding when and why these points fall in line reveals the deep geometric harmony within triangles, and exploring further uncovers even more surprising relationships.
Key Takeaways
- The centroid, orthocenter, and circumcenter are collinear along Euler’s line in most triangles.
- This alignment occurs in all non-equilateral triangles, highlighting intrinsic geometric relationships.
- The points are collinear in acute, right, and obtuse triangles, with specific positions depending on the triangle type.
- The collinearity demonstrates the interconnectedness of key triangle centers through Euler’s line.
- In equilateral triangles, these points coincide at the same location, trivially falling on Euler’s line.

Have you ever wondered how certain special points inside a triangle are connected? These points, like the centroid, orthocenter, and circumcenter, aren’t just random markers; they follow intriguing relationships that reveal the triangle’s hidden harmony. One of the most fascinating discoveries in geometry is Euler’s line, a straight line that passes through these key points, showing that they are more than just individual features—they’re part of a geometric symphony.
Let’s start with the centroid. You can think of it as the triangle’s balancing point, where it would stay perfectly balanced if made of a uniform material. Its properties are quite remarkable: it divides each median into two segments in a 2:1 ratio, with the longer segment always closer to the vertex. This point isn’t just a balance marker; it’s deeply connected to the triangle’s area and how the vertices influence the shape’s distribution. The centroid’s properties help you understand the internal symmetry of the triangle, making it a fundamental reference in various geometric calculations.
The centroid balances the triangle and divides medians in a 2:1 ratio, revealing internal symmetry and shape distribution.
Now, the orthocenter holds a different kind of significance. It’s the point where all three altitudes intersect, and altitudes are perpendicular lines drawn from each vertex to the opposite side. The orthocenter’s significance extends beyond its geometric definition; it’s a vital element in understanding the triangle’s orthogonal relationships and angle properties. For acute triangles, the orthocenter lies inside the triangle, giving insight into the internal angles. In obtuse triangles, it shifts outside, highlighting the triangle’s exaggerated angles. This shifting position underscores the orthocenter’s role in revealing the triangle’s angular structure.
What makes these points even more compelling is that they all line up on Euler’s line. If you draw the centroid, circumcenter, and orthocenter, you’ll see they align perfectly in most triangles—except for some degenerate cases. This alignment isn’t coincidental; it demonstrates a deep geometric unity. The fact that these points fall on a single straight line means that their properties are interconnected, and understanding one can lead to insights about the others. For instance, knowing the properties of the centroid can help you understand the triangle’s balance, while recognizing the orthocenter’s significance can shed light on the orthogonal relationships within the shape.
In essence, Euler’s line reveals that these special points—centroid properties and orthocenter significance—are more than separate features. They are part of a harmonious geometric structure, reminding you that even within a simple triangle, there’s a profound interconnectedness waiting to be uncovered.
Frequently Asked Questions
How Is Euler’s Line Related to Other Triangle Centers?
Euler’s line relates directly to triangle centers through geometric collinearity. When you examine the centroid, orthocenter, and circumcenter, you’ll find they all lie on this single line called Euler’s line. This special collinearity reveals the deep connections among these centers, showing that despite their different roles, they align perfectly in the triangle’s geometry. Understanding this helps you see the hidden order in triangle structures.
Can Euler’s Line Be Constructed Without a Compass and Straightedge?
You can’t accurately construct Euler’s line without a compass and straightedge because it relies on precise points like the circumcenter, centroid, and orthocenter. Using straightedge techniques alone, you might sketch approximate locations, but you won’t get a reliable, exact line. Compass construction helps find midpoints and perpendicular bisectors, which are essential for identifying these centers. So, for a precise Euler’s line, you need both tools.
Does Euler’s Line Exist in Non-Euclidean Geometries?
In non-Euclidean geometries, Euler’s line generally doesn’t exist as it does in Euclidean geometry. You won’t find the same collinear points like the circumcenter, centroid, and orthocenter because the fundamental rules of non-Euclidean geometries differ. If you’re exploring spherical or hyperbolic spaces, these special points don’t align in the same way, so Euler’s line isn’t applicable or definable in those contexts.
Are There Real-World Applications of Euler’s Line?
You’ll find Euler’s line useful in engineering applications and architectural designs. It helps optimize structural stability by understanding the relationship between a triangle’s centroid, orthocenter, and circumcenter. Engineers use this knowledge to create balanced frameworks, while architects incorporate these principles for aesthetic and functional purposes. Recognizing Euler’s line enhances precision in design, ensuring that structures and models are both efficient and visually appealing, making it a valuable tool in real-world construction and design projects.
How Does Euler’s Line Change in Obtuse Versus Acute Triangles?
Did you know that in all triangles, the centroid, circumcenter, and orthocenter are always collinear? In an acute triangle, these points are inside the triangle, forming a neat Euler’s line. But in an obtuse triangle, the line’s configuration shifts; the orthocenter lies outside, affecting line collinearity. This change highlights how the triangle’s shape influences the Euler’s line, revealing different geometric properties.
Conclusion
As you explore Euler’s line, you realize it’s more than just a straight path through a triangle’s special points. It hints at deeper connections waiting to be uncovered. What other secrets lie hidden in these geometric marvels? Keep digging, because the journey doesn’t end here. The line’s mysterious alignment is just the beginning, and who knows what surprising truths you might discover next—if you’re willing to follow where it leads. The next revelation could be closer than you think.