In a cyclic quadrilateral, you’ll find that opposite angles always add up to 180 degrees. This is because each angle is inscribed in a circle, intercepting arcs that together cover the full circle. Fundamentally, the measure of each inscribed angle is half of its intercepted arc, linking angles directly to the circle’s properties. Exploring how these angles relate deepens your understanding of circle geometry, and if you look further, you’ll uncover even more fascinating connections.
Key Takeaways
- Opposite angles in a cyclic quadrilateral are always supplementary, summing to 180 degrees.
- Inscribed angles measure half the arc they intercept, linking angles to circle arcs.
- Opposite angles intercept arcs that together sum to 360 degrees, confirming their supplementary relationship.
- Recognizing these angle properties helps identify and analyze cyclic quadrilaterals in geometric problems.
- The circle connection ensures that all four vertices lie on the same circle, maintaining the cyclic nature.
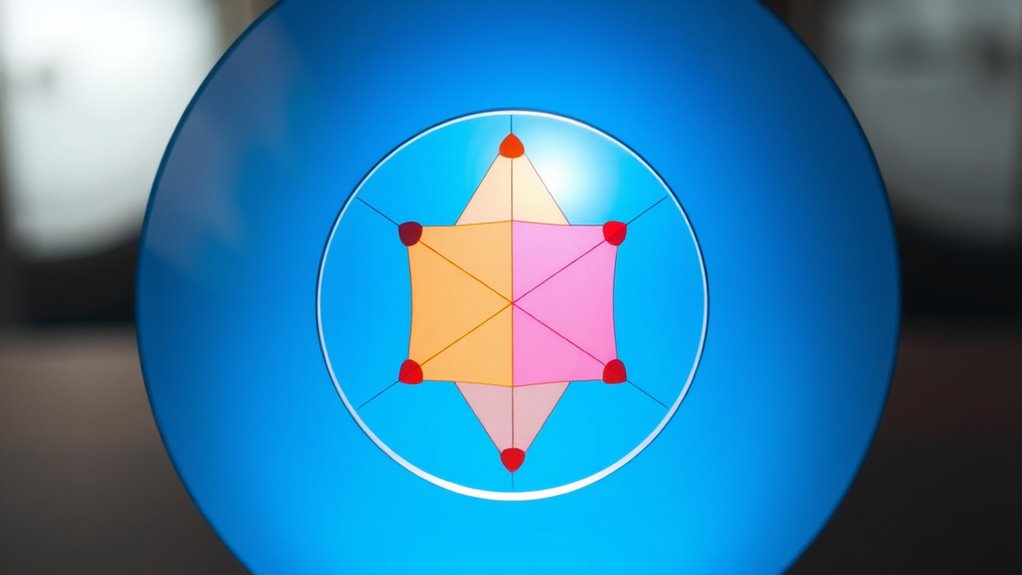
Have you ever wondered what makes a quadrilateral cyclic? It’s a fascinating property that links the shape’s angles to the circle in which it’s inscribed. When a quadrilateral is cyclic, all four vertices lie on the same circle, and this unique arrangement gives rise to specific angle properties that set it apart from other quadrilaterals. To understand this, you need to grasp the concept of inscribed angles—angles formed when two chords intersect at a point on the circle. These angles hold key clues about the relationships within the cyclic quadrilateral.
A quadrilateral is cyclic when all four vertices lie on the same circle, with opposite angles summing to 180 degrees.
In a cyclic quadrilateral, the opposite angles always add up to 180 degrees. This is a direct consequence of the angle properties associated with inscribed angles. When you look at two opposite angles, each inscribed in the circle, you’ll notice that they are supplementary. This means that if you measure one angle, you can find its opposite by subtracting that measurement from 180 degrees. This property is not just a coincidence; it’s rooted in the fact that inscribed angles subtend the same arc or supplementary arcs on the circle. This relationship makes cyclic quadrilaterals unique because it guarantees that their opposite angles are always supplementary, unlike in a general quadrilateral.
To see why this works, think about how inscribed angles relate to their intercepted arcs. An inscribed angle always measures half the measure of its intercepted arc. When you consider two opposite angles in a cyclic quadrilateral, each inscribed angle intercepts an arc that together sums to a full circle, or 360 degrees. Because of this, the inscribed angles are each half of their respective arcs, and the sum of these angles naturally equals 180 degrees. This elegant connection shows why opposite angles in a cyclic quadrilateral are supplementary and highlights the essential role of inscribed angles in understanding circle relationships. Additionally, the concept of circle connectivity underpins the entire structure of cyclic quadrilaterals, making them a fundamental topic in geometry.
Knowing these angle properties helps you identify whether a given quadrilateral is cyclic. If you can verify that the opposite angles sum to 180 degrees, you’ve confirmed its cyclic nature. Furthermore, understanding inscribed angles allows you to solve problems involving angles and arcs more efficiently, as they provide a direct link between the shape’s geometry and the circle’s properties. Recognizing these relationships deepens your insight into circle geometry and enhances your ability to analyze complex figures. So, when you see a quadrilateral with opposite angles adding up to 180 degrees, you now understand that it’s likely a cyclic quadrilateral, with inscribed angles playing a vital role in its geometric behavior.
Frequently Asked Questions
How Can Cyclic Quadrilaterals Be Constructed Using Only a Compass and Straightedge?
To construct a cyclic quadrilateral with a compass and straightedge, start by drawing a circle and marking four points on it using straightedge techniques. Connect the points with straight lines to form the quadrilateral. Guarantee that opposite angles are supplementary by adjusting points along the circle’s circumference. Use your compass to verify equal angles or lengths if needed. This method relies on precise compass constructions and straightedge techniques to create the desired cyclic quadrilateral.
What Are the Real-World Applications of Cyclic Quadrilaterals in Engineering?
Ever wondered how engineers guarantee bridges stay stable? Cyclic quadrilaterals help in bridge design by ensuring structural stability through precise angle calculations. They allow engineers to model load distributions and optimize support placements, making structures safer and more durable. You can see their application in arches and trusses, where understanding circle connections and opposite angles ensures that forces are evenly distributed, preventing collapse and enhancing overall safety.
Are There Any Special Properties of Cyclic Quadrilaterals With Right Angles?
If a cyclic quadrilateral has a right angle, you’ll notice that its opposite angles are also right angles, making the figure a rectangle. This property helps you identify right-angled cyclic quadrilaterals easily. When you see a quadrilateral inscribed in a circle with one right angle, you can immediately determine that its opposite angles are equal and also right. This simplifies many geometric proofs and problem-solving scenarios.
How Does the Concept of Cyclic Quadrilaterals Extend to Three-Dimensional Geometry?
In three-dimensional geometry, cyclic quadrilaterals extend through spherical geometry, where four points lie on a common sphere, creating a spherical cyclic quadrilateral. You’ll notice that spherical cyclicity involves great circles and spherical angles, which differ from flat-plane properties. This three-dimensional cyclicity helps analyze complex shapes, such as polyhedra, by understanding how these spherical quadrilaterals relate to the circumscribed sphere, enriching your comprehension of spatial relationships.
What Are Common Mistakes to Avoid When Proving a Quadrilateral Is Cyclic?
Remember, “measure twice, cut once,” especially when proving a quadrilateral is cyclic. Avoid common mistakes like angle misproofs, where you miscalculate or assume angles without proper reasoning, and opposite side errors, which occur when you incorrectly identify pairs of sides as opposite. Always verify that opposite angles are supplementary or that the vertices lie on a common circle. Double-check your reasoning to make sure your proof is solid.
Conclusion
Now that you see how opposite angles in cyclic quadrilaterals sum to 180°, you realize their unique connection to circles. Unlike other quadrilaterals, they’re bound by circular rules that reveal fascinating properties. This contrast highlights how geometry’s rules intertwine, revealing elegant relationships. So, next time you spot a quadrilateral inscribed in a circle, remember: its opposite angles tell a story of harmony between angles and circles, inviting you to explore more geometric wonders.