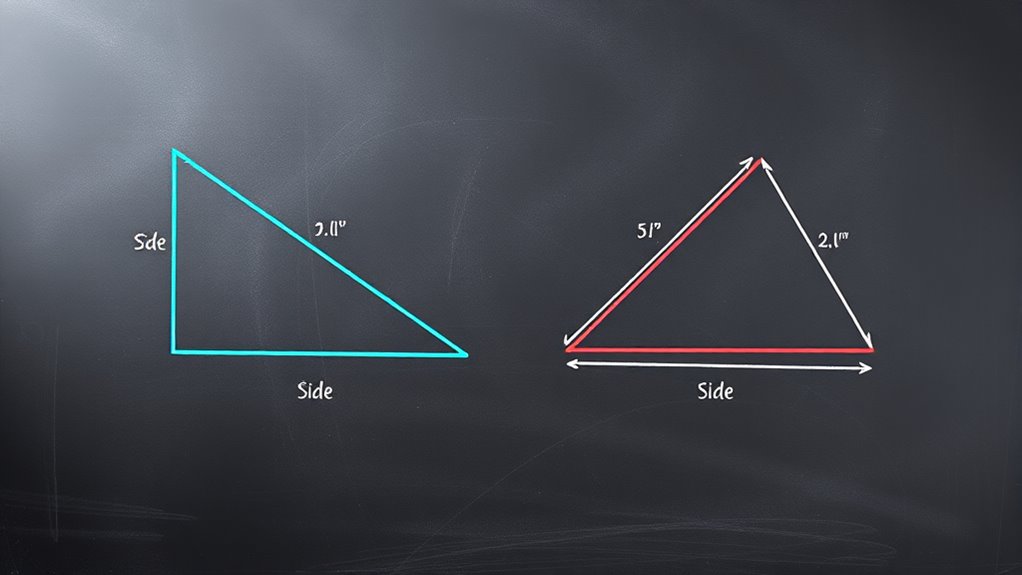
The Side-Side-Side (SSS) rule works because if three sides of one triangle are exactly equal to three sides of another, the triangles must have the same shape and size. This relies on the properties of triangles and the idea that fixing three sides determines a unique triangle. Other rules like SAS or ASA use angles and sides to confirm congruence. Keep exploring to understand how these rules guarantee triangles are identical every time.
Key Takeaways
- The SSS rule is valid because if three sides of one triangle equal three sides of another, their shapes must be identical.
- Congruence rules like SSS and SAS are justified through geometric properties and logical proofs.
- Side lengths determine a triangle’s shape uniquely, making SSS a reliable criteria for congruence.
- Other rules, such as SAS and ASA, rely on established angle-side relationships proven through geometric theorems.
- These rules ensure that matching sides and angles lead to identical triangles, confirming congruence rigorously.

Congruent triangles are triangles that are exactly the same size and shape, meaning all their corresponding sides and angles are equal. When you see two triangles that match perfectly, they are congruent, and you can confidently say they are identical in every aspect. Understanding congruence is fundamental in geometry because it helps you establish relationships between shapes without measuring every side and angle repeatedly. To prove that two triangles are congruent, you often rely on specific rules, such as Side-Side-Side (SSS), Side-Angle-Side (SAS), and others. These rules are based on geometric proofs that demonstrate congruence using the properties of the triangles involved.
One key concept to grasp when working with triangles is triangle similarity. Unlike congruence, similarity indicates that two triangles have the same shape but not necessarily the same size. They have equal corresponding angles and proportional sides. Recognizing similarity is *essential* because it allows you to compare triangles and deduce unknown measurements through ratios. When two triangles are similar, you can set up proportions between their corresponding sides, which simplifies many geometric problems. This process is often used in geometric proofs to establish relationships between different parts of a figure, especially when proving congruence or similarity.
Understanding geometric properties is crucial because it underpins the logical reasoning used in proofs and helps you justify why certain rules, like SSS and SAS, hold true. These proofs serve as the backbone for validating the rules that determine triangle congruence. These proofs involve logical reasoning, the application of postulates, and theorems that help you justify why two triangles are congruent. For example, when using the SSS rule, you demonstrate that all three pairs of corresponding sides are equal, leading to the conclusion that the triangles are congruent. Similarly, SAS involves showing two sides and the included angle are equal, which also guarantees congruence. These proofs rely on fundamental properties of triangles and the relationships between their sides and angles, making your conclusions rigorous and reliable.
Frequently Asked Questions
Can Two Triangles Be Congruent With Different Orientations?
Yes, two triangles can be congruent with different orientations. When you perform a triangle rotation or a congruence transformation, the triangles stay congruent because their side lengths and angles remain the same. These transformations, like rotating or flipping a triangle, change its orientation without altering its shape or size. So, even if they look different due to their orientation, the triangles are still congruent because they have identical corresponding sides and angles.
How Does Congruence Relate to Triangle Similarity?
Congruence means your triangles are exactly the same size and shape, with all angles and sides matching, while similarity involves having the same shape but different sizes. You relate them through angle correspondence, where angles in one triangle match with angles in the other. Using similarity criteria, like AA, SAS, or SSS, helps determine if triangles are similar, but for congruence, you need all sides and angles to correspond exactly.
Are There Any Exceptions to the SSS Rule?
You might think the SSS rule has no exceptions, but actually, it doesn’t account for the triangle inequality. If the three sides don’t satisfy this, the triangle isn’t valid, so SSS can’t guarantee congruence. Remember, congruence criteria like SSS only work when the sides form a real triangle. So, in a way, the triangle inequality is the sneaky exception that keeps SSS from being foolproof in all cases.
How Do I Prove Triangles Are Congruent in Real-World Problems?
To prove triangles are congruent in real-world problems, you match corresponding sides and angles. First, identify the side matching and angle correspondence, such as labeling sides and angles consistently. Then, use rules like SSS, SAS, or ASA to show the triangles are congruent. Confirm that the pairs of sides and angles you’ve matched are equal, ensuring your proof is solid and based on clear correspondence.
What Are Some Common Mistakes When Using SSS?
You might think of using SSS as your trusty time machine, but watch out for common mistakes. If there’s an angle mismatch or incorrect side lengths, your proof falls apart—like a broken compass in a storm. Don’t assume all sides are equal without double-checking measurements. Always verify side lengths carefully and confirm the triangles’ corresponding angles match. Otherwise, your conclusion about congruence might be as off as an ancient miscalculation.
Conclusion
Now that you’ve explored the rules for congruent triangles, imagine each triangle as a perfectly matched puzzle piece, fitting seamlessly into place. The Side-Side-Side rule is like a gentle whisper confirming their unity, guiding you to see the harmony in shapes. Trust these clues as your map through geometric wonders. With this knowledge, you’ll navigate triangles with confidence, appreciating their quiet symmetry and the beauty of their unbreakable bonds—like a serene dance of perfectly matched partners.