In trigonometry, sine, cosine, and tangent are ratios that relate the angles of a right triangle to its sides. Sine compares the opposite side to the hypotenuse, cosine compares the adjacent side to the hypotenuse, and tangent compares the opposite side to the adjacent. These functions help you understand the relationship between angles and side lengths. If you keep exploring, you’ll discover how these concepts connect to larger concepts like the unit circle and real-world applications.
Key Takeaways
- Sine, cosine, and tangent are primary trigonometric ratios relating angles to side lengths in right triangles.
- Sine is opposite over hypotenuse; cosine is adjacent over hypotenuse; tangent is opposite over adjacent.
- These ratios help determine unknown side lengths or angles in triangles.
- The unit circle visually represents how these ratios vary with different angles.
- Trigonometry is essential in fields like engineering, navigation, and physics for analyzing spatial relationships.
Understanding the Right Triangle and the Basics of Trigonometry
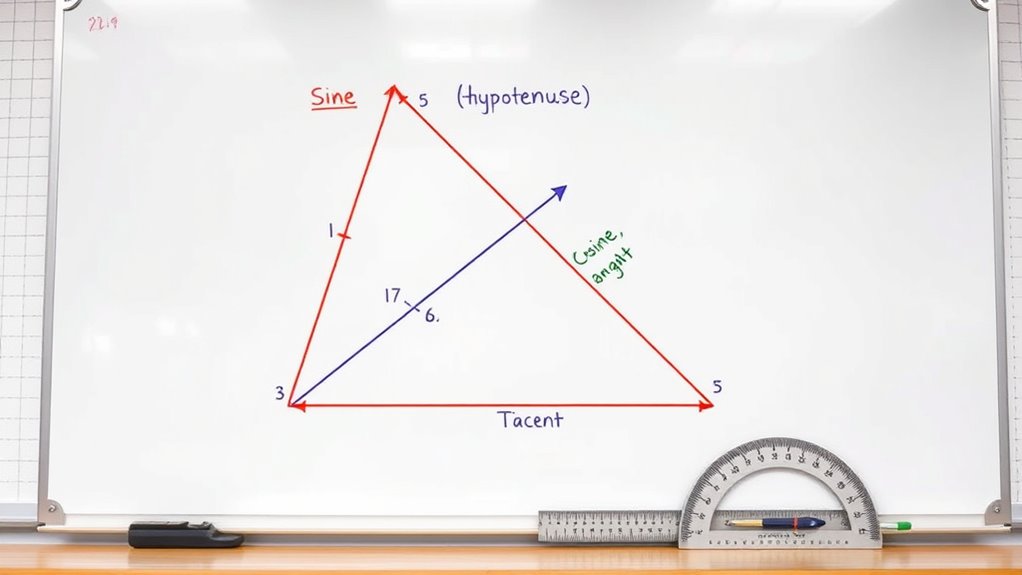
A right triangle is a triangle that has one angle measuring 90 degrees. This special triangle helps you understand the basics of trigonometry because the other two angles are complementary, totaling 90 degrees. The side opposite the right angle is called the hypotenuse, while the other two sides are legs. When studying angle measurement, you’ll see how each angle relates to side lengths. The unit circle, a circle with a radius of one, provides a helpful way to visualize these relationships. It allows you to see how angles in a right triangle correspond to specific points on the circle. This connection simplifies understanding how angles and side ratios are linked, laying the foundation for calculating sine, cosine, and tangent. Additionally, trigonometric functions are used extensively in fields like engineering, physics, and computer graphics to solve real-world problems.
How to Calculate Sine, Cosine, and Tangent in a Triangle

To calculate sine, cosine, and tangent in a right triangle, start by identifying the sides relative to a specific angle. The sine is the ratio of the length of the opposite side to the hypotenuse, while cosine compares the adjacent side to the hypotenuse. Tangent is the ratio of the opposite side to the adjacent side. These are called angle ratios because they describe how side lengths relate to each other for a given angle. You can also use the unit circle, where the coordinates of a point on the circle correspond to these ratios for different angles. This approach helps visualize how sine, cosine, and tangent vary across all angles, not just those in right triangles. Understanding these ratios is fundamental to applying trigonometry in more complex problems. Additionally, sound healing science offers insights into the influence of frequencies on our well-being, which can be related to the precise measurements in trigonometry when analyzing wave patterns.
Practical Uses of These Functions in Real-World Situations

Practical applications of sine, cosine, and tangent functions are everywhere in everyday life, helping you solve real-world problems efficiently. In engineering applications, these functions are essential for designing structures, analyzing forces, and calculating angles in machinery. They guarantee safety and precision in construction projects. In navigation techniques, these functions help you determine directions, calculate distances, and plot courses accurately. For example, when using a compass or GPS, understanding how to apply trigonometry allows you to find your position or plan best routes. Whether you’re an engineer, navigator, or hobbyist, mastering these functions equips you with tools to interpret and solve spatial problems, making complex tasks manageable and precise. Trigonometry’s practical uses are integral to many fields that rely on accurate measurement and directional understanding. Additionally, these functions are vital in creating home theatre projectors with precise image alignment and calibration for optimal viewing experiences.
Frequently Asked Questions
How Do Trigonometric Functions Relate to the Unit Circle?
When you explore the unit circle visualization, you see how trigonometric functions relate to angles. By using angle measurement techniques, you assign specific points on the circle to measure sine, cosine, and tangent values. As you rotate around the circle, these functions correspond to the y-coordinate, x-coordinate, and their ratio, respectively. This makes understanding how angles connect to ratios much clearer, helping you grasp their fundamental relationships.
What Are the Common Mistakes When Calculating Sine, Cosine, and Tangent?
Ever wonder why your calculations go awry? You might be falling into common traps like angle confusion, mixing degrees and radians, or making calculator errors by forgetting to set it correctly. These slip-ups can lead to incorrect sine, cosine, and tangent values. Stay alert, double-check your units, and verify your calculator is in the right mode. Avoid these mistakes, and you’ll master trigonometric functions with confidence.
How Can I Memorize the Values of Trigonometric Functions?
To memorize the values of trigonometric functions, you can use effective memorization techniques, like creating mnemonic devices. For example, develop catchy phrases or patterns that help you recall key values, especially at special angles like 30°, 45°, and 60°. Repetition and visual aids also boost your memory. Practice regularly, and over time, these values will become second nature, making your calculations quicker and more accurate.
What Is the Significance of Reference Angles in Trigonometry?
Imagine standing at the origin, and your angle measurement points you into different parts of a circle—this is where reference angles matter. They’re the smallest angles between your position and the x-axis, helping you determine the sign and value of trigonometric functions across quadrants. Reference angles simplify quadrant determination, making it easier to find accurate values without memorizing every angle, especially for complex or unfamiliar measurements.
How Do Trigonometric Identities Simplify Complex Calculations?
To simplify complex calculations, you use trigonometric identities, which are equations that relate different trig functions. These identities help you rewrite complicated expressions into simpler forms, making calculations easier and faster. By applying identities like Pythagorean, reciprocal, or angle sum formulas, you reduce the risk of errors and save time, especially when solving equations or evaluating functions in more advanced problems.
Conclusion
Now that you understand the fundamentals of sine, cosine, and tangent, you’re ready to explore even more complex problems. These functions hold the key to revealing hidden angles and distances in the world around you. But remember, as you dive deeper, you’ll discover that there’s always more to uncover—secrets hidden in the angles you see every day. Are you ready to uncover what lies beyond the basics? The next step awaits.