To prove that the base angles of an isosceles triangle are equal, you can draw the median from the vertex angle to the base, dividing the triangle into two smaller triangles. These are congruent because they share a side, have equal sides, and a side of equal length. This congruence shows that the base angles are equal. Exploring this proof helps you understand the symmetry behind isosceles triangles and why their angles behave this way.
Key Takeaways
- Draw median AD from vertex A to midpoint D of the base BC, creating two smaller triangles △ABD and △ACD.
- Since AB equals AC by the isosceles triangle definition, and D is midpoint, BD equals DC.
- The triangles △ABD and △ACD share side AD and have all three sides equal via SSS congruence.
- Congruence of △ABD and △ACD implies their corresponding angles at B and C are equal.
- Therefore, the base angles at B and C are congruent, proving they are equal.

In an isosceles triangle, two sides are equal by definition, and this symmetry leads to a fundamental property: the angles opposite those sides are also equal. When you examine such a triangle, you’ll notice that the two equal sides are called the legs, and the angle where they meet is the vertex angle. The base angles are the angles opposite the equal sides. The goal of this proof is to show that these base angles are always equal, and you can do this by leveraging the concept of triangle congruence.
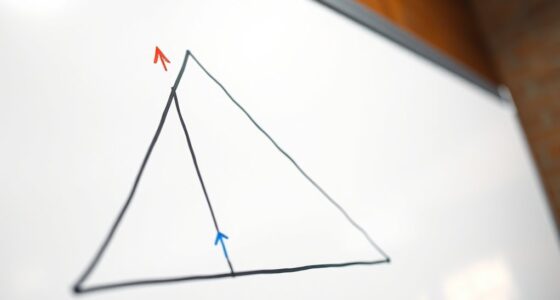
Start by considering your isosceles triangle, label it ABC, with sides AB and AC being equal. The vertex angle is at A, with base angles at B and C. To prove that angles at B and C are equal, you can draw the median from the vertex A to the midpoint of BC. Let’s call the midpoint D. By drawing AD, you create two smaller triangles within the original: △ABD and △ACD.
Drawing the median from A to D in an isosceles triangle proves the base angles are equal through triangle congruence.
Next, observe that since AB equals AC, and AD is common to both triangles, you have two pairs of equal sides: AB equals AC, and AD is shared. Additionally, since D is the midpoint of BC, BD is equal to DC. Now, look at triangles △ABD and △ACD: they share side AD, and the pairs of sides AB and AC are equal by the initial assumption of the triangle being isosceles. Moreover, BD equals DC because D is the midpoint.
Using the Side-Side-Side (SSS) triangle congruence criterion, you see that △ABD is congruent to △ACD. Because these triangles are congruent, their corresponding angles are equal. Specifically, angle ABD corresponds to angle ACD. These are the base angles at B and C, respectively. As a result, you’ve shown that the base angles are equal because the two triangles, created through the median, are congruent.
This demonstration hinges on the principle of triangle congruence, which ensures the equality of corresponding parts. It’s a straightforward yet powerful approach that confirms the symmetry inherent in isosceles triangles. The key point is that the equal sides lead directly to the equality of the vertex angles and the congruence of the two smaller triangles, which in turn guarantees the equality of the base angles. This proof not only verifies the property but also deepens your understanding of how symmetry and congruence work together in geometry.
Additionally, understanding the role of angle bisectors in such proofs can provide further insight into triangle properties and congruence relationships.
Frequently Asked Questions
Can the Proof Be Applied to Obtuse Isosceles Triangles?
Yes, you can apply the proof to obtuse isosceles triangles. The angle properties that state the base angles are equal hold true regardless of whether the triangle is acute, right, or obtuse. Since triangle classifications are based on angles, your understanding of isosceles triangles remains consistent. Just remember, the key is that two sides are equal, and the base angles are equal, no matter the triangle’s overall size or angle measures.
Are There Alternative Methods to Prove Equal Base Angles?
Yes, you can use alternative methods like angle bisectors and symmetry properties to prove equal base angles. Drawing an angle bisector from the vertex opposite the base splits the triangle into two equal parts, highlighting symmetry. This approach works for all isosceles triangles, including obtuse ones, because it relies on fundamental geometric principles rather than specific angle measures, offering a versatile proof method.
How Does This Proof Relate to Other Triangle Congruence Theorems?
Imagine your triangle bursting into a story of friendship! This proof links tightly to triangle congruence theorems like SAS and ASA, which use geometric constructions and triangle similarity to show that angles or sides are equal. Just as friendships form bonds, these theorems connect triangles through shared sides and angles, confirming their congruence and revealing that the base angles are equal, solidifying the triangle’s perfect harmony.
What Are Common Mistakes When Proving Equal Base Angles?
You should watch out for misapplied assumptions and overlooked cases when proving equal base angles. For example, assuming the triangle is isosceles without establishing it can lead to errors. Also, neglecting to take into account different configurations or special cases, like right triangles, might cause you to overlook exceptions. Always verify that your conditions truly apply, and don’t make assumptions without proper justification to ensure your proof holds.
Is the Proof Valid in Non-Euclidean Geometries?
Think of non-Euclidean geometries as different maps of the same world; your usual proof methods might not fit. In these geometries, the classic proof of equal base angles isn’t always valid because the rules differ. You’d need alternative proof methods tailored to the specific non-Euclidean system. So, always check which geometry you’re working with to verify your proof holds true, or seek methods suited for that framework.
Conclusion
Now that you’ve explored the proof, it’s clear that the base angles of an isosceles triangle are indeed equal. This isn’t just a coincidence; it’s a proven fact supported by geometric principles. Next time you see an isosceles triangle, remember how its symmetry guarantees these equal angles. Isn’t it fascinating how mathematics reveals such elegant truths? Keep questioning and exploring—who knows what other geometric secrets you’ll uncover!