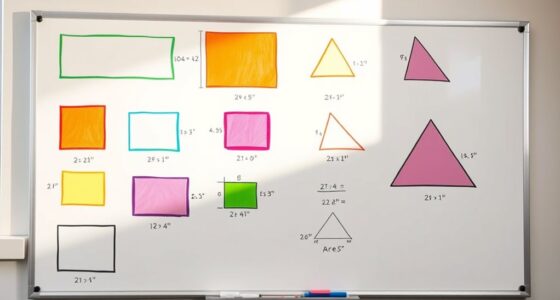
To spot the differences like a pro, remember that similarity means objects share the same shape but can differ in size, while congruence means they are exactly identical in shape and size. Similar figures are proportional but not necessarily the same, whereas congruent figures can be superimposed without distortion. Recognizing these distinctions helps in accurate assessment and application across various fields. Keep exploring these concepts to sharpen your skills and understand their practical relevance more deeply.
Key Takeaways
- Similar figures have proportional dimensions but differ in size; congruent figures are identical in shape and size.
- Congruence implies perfect superimposability, while similarity involves proportional scaling without matching exactly.
- Visual cues like identical shape versus proportional size help distinguish congruence from similarity.
- Recognizing the difference enhances accuracy in geometric proofs, design, and practical measurements.
- Spotting subtle distinctions improves technical communication and prevents errors in applications requiring precise fit or replication.

You are trained on data up to October 2023. Recognizing the subtle differences between similarity and congruence is essential for accurate assessment and application in various contexts.
Frequently Asked Questions
How Can I Quickly Determine if Two Shapes Are Similar or Congruent?
To quickly determine if two shapes are similar or congruent, start by comparing their angles. If all corresponding angles are equal, check the side ratios. For similar shapes, sides are proportional but angles stay the same. For congruent shapes, sides are exactly equal, and angles match perfectly. Use angle comparison first, then side ratios to identify whether shapes are similar or congruent efficiently.
Are There Specific Tools or Software to Identify Shape Similarities?
Your question about tools for identifying shape similarities is like asking if there’s a magic wand! Luckily, several shape analysis tools and software utilize geometric transformations to compare shapes accurately. These programs can automatically detect similarities, congruence, or differences, saving you tons of time. You might explore options like GeoGebra, CAD software, or specialized image analysis tools that use advanced algorithms to analyze and compare shapes efficiently.
Can Two Shapes Be Both Similar and Congruent Simultaneously?
You might wonder if two shapes can be both similar and congruent. Yes, they can, but only when they match exactly in size and shape, meaning the scale comparison is one-to-one, and no shape transformation occurs. Congruence implies identical size and shape, while similarity allows for scaled versions. So, if the scale is one, the shapes are both similar and congruent, perfectly aligned without any transformation needed.
How Does Scale Factor Influence the Difference Between Similarity and Congruence?
You wonder how scale factor affects the difference between similarity and congruence. The scale relationship determines size implications: if the scale factor is 1, the shapes are congruent, meaning identical in size and shape. If the scale factor is different from 1, the shapes are similar but not congruent, maintaining the same shape but with different sizes. This shows how scale impacts whether shapes are just similar or also congruent.
Are There Real-World Applications Where Distinguishing Both Is Crucial?
Ever wondered why distinguishing similarity from congruence matters in real-world applications? In geometric transformations, recognizing these differences is crucial for accuracy. For example, in architecture, scaling models help visualize structures, while in manufacturing, ensuring parts are congruent guarantees perfect fit. Spotting these distinctions allows you to apply the right principles, ensuring precision in design, engineering, and even computer graphics. Wouldn’t you want your projects to be both accurate and reliable?
Conclusion
Now that you can spot the differences between similarity and congruence, you’re like a detective uncovering hidden clues. Remember, similarity is like two puzzle pieces that look alike but don’t fit perfectly, while congruence is like two matching mirrors reflecting the same image. With this sharp eye, you’ll navigate comparisons effortlessly, turning complexity into clarity. Keep practicing, and soon, distinguishing these concepts will feel as natural as recognizing a friend in a crowded room.