In understanding sine, cosine, and tangent, you discover how these ratios relate angles to triangle sides and points on the unit circle. Sine and cosine show vertical and horizontal distances, while tangent indicates slope. These ratios repeat periodically as angles change, helping you analyze wave patterns and slopes. Mastering these basics offers a foundation for solving triangle problems and real-world situations — and if you keep exploring, you’ll uncover even more about their fascinating applications.
Key Takeaways
- Sine, cosine, and tangent are fundamental ratios that relate angles to side lengths in right triangles.
- The unit circle visually demonstrates how these ratios change with angle rotation and repeats periodically.
- Sine corresponds to the vertical coordinate, cosine to the horizontal, and tangent to the ratio of sine over cosine.
- These ratios help solve triangle problems and model wave patterns in various real-world applications.
- Understanding their periodic nature is essential for predicting ratio values at any angle.

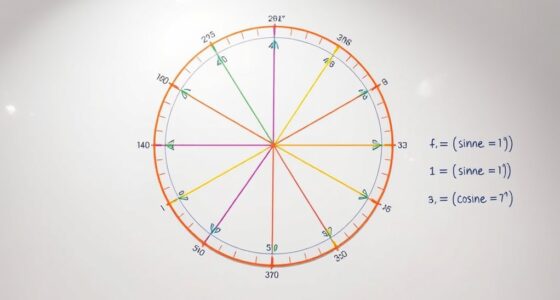
Trigonometry is the branch of mathematics that studies the relationships between the angles and sides of triangles. When you’re starting out, one of the most helpful tools is the unit circle. This circle, with a radius of one, serves as a foundation for understanding how angles correspond to specific ratios. As you move around the circle, you’ll see how the coordinates of points on the circle relate directly to the trigonometric ratios: sine, cosine, and tangent. These ratios are essential because they connect the angles within a triangle to the lengths of its sides, giving you a systematic way to analyze and solve problems involving triangles.
Imagine you’re standing at the center of the unit circle, and you measure an angle from the positive x-axis. The point where the angle intersects the circle has coordinates that are directly tied to the sine and cosine of that angle. Specifically, the x-coordinate equals the cosine, and the y-coordinate equals the sine. This visualization makes it easier to grasp how these ratios change as you rotate around the circle. For a given angle, the cosine tells you the horizontal distance from the origin, while the sine indicates the vertical distance. These are your primary trigonometric ratios, and they’re fundamental in understanding the properties of triangles and periodic functions.
Additionally, understanding the unit circle helps you see the periodic nature of these ratios and how they repeat as angles increase or decrease beyond 360 degrees. The tangent ratio, on the other hand, is derived from sine and cosine. It’s equal to the sine divided by the cosine, representing the ratio of the vertical to horizontal components. When you understand how sine and cosine relate to the unit circle, you can see why tangent corresponds to the slope of the line connecting the origin to a point on the circle at a given angle. This ratio helps you understand the steepness of a line and is *integral* in solving problems involving angles of elevation, depression, or slopes in real-world situations.
Frequently Asked Questions
How Are Sine, Cosine, and Tangent Related to Each Other?
You see that sine, cosine, and tangent are all related through angle relationships and reciprocal functions. Sine is the ratio of the opposite side to the hypotenuse, while cosine is the adjacent side over the hypotenuse. Tangent compares the opposite to the adjacent side. These functions connect through reciprocal relationships: cosine is the reciprocal of secant, sine of cosecant, and tangent of cotangent, making them integral parts of trigonometry.
What Real-World Applications Use Trigonometric Functions?
You use trigonometric functions every day, often without realizing it. In engineering design, sine and cosine help calculate angles and forces, ensuring structures are safe. Navigation systems rely on tangent and sine to determine positions and routes, guiding you accurately from place to place. These functions bridge abstract math and real-world problems, making your travels smoother and your creations more precise.
How Do I Memorize the Basic Trigonometric Identities?
To memorize basic trigonometric identities, use mnemonic techniques like “SOH-CAH-TOA” for sine, cosine, and tangent ratios. Create flashcards for formula derivations, breaking them down step-by-step to understand their origins. Practice regularly, quiz yourself, and relate identities to real-world problems. Repetition helps reinforce memory, making these formulas second nature. Visual aids like charts or diagrams also improve recall and understanding.
What Are the Common Mistakes Beginners Make in Trigonometry?
You often mistake common misconceptions for simple truths, stumble over calculation errors, and overlook the importance of unit consistency. Beginners tend to confuse sine, cosine, and tangent functions, forget to verify their angles are in degrees or radians, and rush through calculations without checking their work. To avoid these mistakes, double-check your formulas, slow down during calculations, and clarify your understanding of each trigonometric concept.
How Does the Unit Circle Help in Understanding Trigonometry?
The unit circle helps you understand trigonometry by linking angles to their sine and cosine values through angle measurement. When you visualize the circle, you see how different angles correspond to points on its circumference, making it easier to grasp how sine and cosine functions behave. This visual tool simplifies complex calculations and deepens your understanding of the relationships between angles and their trigonometric values.
Conclusion
Now that you’ve uncovered the basics of sine, cosine, and tangent, you’re like a traveler holding a map to a hidden landscape. These functions are your compass, guiding you through the intricate maze of angles and triangles. With each step, you’ll see how they intertwine like threads in a tapestry, revealing the beauty of geometry. Keep exploring, and you’ll soon master the language that unseals the secrets of the universe’s angular dance.